Pankaj Tanwar
Published on

Scalability Challenge - How to remove duplicates in a large data set (~100M) ?

––– views

Dealing with large datasets is often daunting. With limited computing resources, particularly memory, it can be challenging to perform even basic tasks like counting distinct elements, membership check, filtering duplicate elements, finding minimum, maximum, top-n elements, or set operations like union, intersection, similarity and so on.

Real World Problem

Almost every mobile app has push notification feature. We need to design a way which guards sending multiple push notifications to the same user for the same campaign.

For Reference :

  • Push notification -

Push notifications are sent to the users device based on push notification token generated by their mobile device.

  • Size of token -

32B to 4KB

  • Assume total Users -

~100 M

  • Additional Details -

  1. It’s non-performant for us to index push tokens or use them as the primary user key.

  2. If user uninstalls the app and subsequently again installs the same app, and then creates a new user profile in the same device. Normally, the mobile platform will generate a new push notif token BUT that's not guaranteed always. For a smaller number of cases, we can end up having multiple user profiles with the same push notif token.

Now, to avoid sending multiple notification to same device, we need to filter out those smaller number of duplicate push notif tokens.

Memory required to filter 100 MN tokens = 100M x 256 = ~25 GB

The Solution

Bloom Filter

Bloom Filters are data structures used to efficiently answer queries when we do not have enough "search key" space to handle all possible queries.

How Bloom Filter Works?

  1. Allocate a bit array of size m
  2. Choose k independent hash functions h(x) whose range is [ 0 .. m-1 ]
  3. For each data element, compute hashes and turn on bits
  4. For query q , apply hashes and check if all the corresponding bits are ‘on’

If all the corresponding bits are 'on' means this is duplicate value.

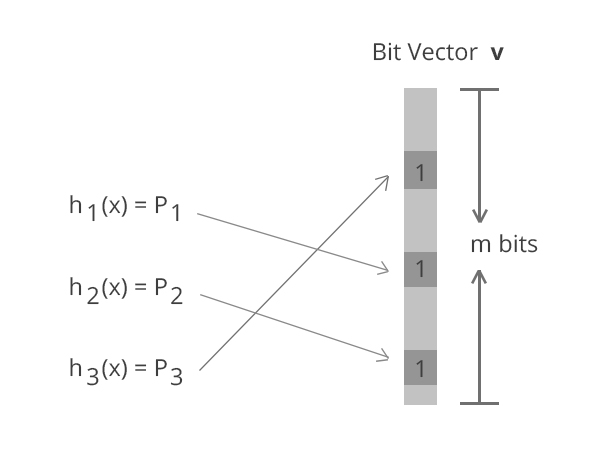
bloom-filter.jpg

NOTE : Bits might be turned ‘on’ by hash collisions leading to false positives

What is the error rate and Memory requirement in bloom filter ?

With m bits, k hash functions, n input strings, we need to the false positive probability (hash collisions).

Probability of setting a bit using a hash function in m bits -

1m\frac{1}{m}

Now, Probability of NOT setting a bit -

(1−1m)(1 - \frac{1}{m})

As we pass it to k hash functions & we have n input strings so the probability of a bit is not being set after passing it to n input strings and k hash functions is -

p=(1−1m)kn{p} = (1 - \frac{1}{m})^{kn}

Now, the probability of getting error/ hash collision (by mistake setting a bit) for k hash functions is

p=(1−(1−1m)kn)k≈(1−e(−knm))k{p} = {(1 - (1 - \frac{1}{m})^{kn})^k} \approx (1 - e^{(-\frac{kn}{m})})^k

for minimising error rate -

dpdk→0\frac{dp}{dk} → {0}

Now,

k=mn×ln(2){k} = \frac{m}{n} \times {ln \hspace{0.2cm} (2)}
  • Size of bit array-
m=−n×(lnp)(ln2)2{m} = - \frac{n \times (ln \hspace{0.2cm} p)}{(ln \hspace{0.2cm} 2)^2}
  • Memory required for 100 Million push tokens with 0.001 error probability -
m=−100000000×(ln0.001)(ln2)2≈171MB{m} = - \frac{100000000 \times (ln \hspace{0.2cm} 0.001)}{(ln \hspace{0.2cm} 2)^2} \approx {171 MB}

This is massive improvement from 25 GB to 171 MB (reducing memory requirements by ~98%)

Applications of Bloom Filters

  1. Facebook uses bloom filters for typeahead search, to fetch friends and friends of friends to a user typed query.

  2. MakeMyTrip uses bloom filters for personalised discount offers based on user data and behaviour instead of calculating category ( eg - loyalCustomer, newBusCustomer, newFlightCustomer) for their ~70M unique customers

  3. One Hit Wonder

IMPORTANT

Hash functions for Bloom filter should be independent and uniformly distributed. Cryptographic hashes like MD5 or SHA-1 are not good choices for performance reasons. Some of the suitable fast hashes are MurmurHash, FNV hashes andJenkin’s Hashes which are faster (~10x faster), distributed and independent.

Thanks for reading.

Source - Suresh Kondamudi's Discussion (CleverTap )

Tweet this article